Raciocínio Lógico - Testes 3

TESTE DE RACIOCÍNIO LÓGICO – PARTE 03

01- Pedro e Paulo saíram de suas respectivas casas no mesmo instante, cada um com a intenção de visitar o outro. Ambos caminharam pelo mesmo percurso, mas o fizeram tão distraidamente que não perceberam quando se cruzaram. Dez minutos após haverem se cruzado, Pedro chegou à casa de Paulo. Já Paulo chegou à casa de Pedro meia hora mais tarde (isto é, meia hora após Pedro ter chegado à casa de Paulo). Sabendo que cada um deles caminhou a uma velocidade constante, o tempo total de caminhada de Paulo, de sua casa até a casa de Pedro, foi de:

a) 60 minutos

b) 50 minutos

c) 80 minutos

d) 90 minutos

e) 120 minutos

Raciocínio Lógico - Testes 2

TESTE DE RACIOCÍNIO LÓGICO QUANTITATIVO –  02

01- Na Mega-Sena são sorteadas seis dezenas de um conjunto de 60 possíveis (as dezenas sorteáveis são 01, 02, ... , 60). Uma aposta simples (ou aposta mínima), na Mega-Sena, consiste em escolher 6 dezenas. Pedro sonhou que as seis dezenas que serão sorteadas no próximo concurso da Mega-Sena estarão entre as seguintes: 01, 02, 05, 10, 18, 32, 35, 45. O número mínimo de apostas simples para o próximo concurso da Mega-Sena que Pedro deve fazer para ter certeza matemática que será um dos ganhadores caso o seu sonho esteja correto é:

a) 8

b) 28

c) 40

d) 60

e) 84

Raciocínio Lógico - Testes 1

Novos testes com gabarito, ótimo para estudo de raciocínio lógico nível MPU, bom estudo a todos!!!

TESTE DE RACIOCÍNIO LÓGICO QUANTITATIVO – 01

01- Três rapazes e duas moças vão ao cinema e desejam sentar-se, os cinco, lado a lado, na mesma fila. O número de maneiras pelas quais eles podem distribuir-se nos assentos de modo que as duas moças fiquem juntas, uma ao lado da outra, é igual a:

a) 2

b) 4

c) 24

d) 48

e) 120

Probabilidade - União de dois eventos

Para um melhor entendimento da matéria, será explicado em dois exemplos. No primeiro exemplo a intersecção entre os eventos é vazia, no segundo não.

Exemplo 1

Ao lançarmos um dado, qual é a probabilidade de obtermos um número menor que 3 ou maior que 4?

Como sabemos, neste exemplo o espaço amostral é composto de seis elementos descritos abaixo:

S = { 1, 2, 3, 4, 5, 6 }

Chamemos de A o evento que representa a ocorrência de números menores que 3:

Permutação e Permutação com Letras e Números

Permutação de elementos repetidos deve seguir uma forma diferente da permutação, pois elementos repetidos permutam entre si. Para compreender como isso acontece veja o exemplo abaixo:

A permutação da palavra MATEMÁTICA ficaria da seguinte forma:

Sem levar em consideração as letras (elementos) repetidas, a permutação ficaria assim:

P₁₀ = 10! = 3.628.800

Analise Combinatória, Anagramas, Arranjos e Combinações

Análise combinatória é um estudo realizado na matemática e na lógica, responsável pela análise das possibilidades e das combinações. Observe alguns exemplos de exercícios que são resolvidos utilizando análise combinatória.

Se quiser saber quantos números de quatro algarismos são formados com os algarismos 1, 2, 3, 4, 5, 6, 7 e 9, é preciso aplicar as propriedades da análise combinatória.

Um homem possui cinco camisas, quatro calças, três paletós e dois pares de sapatos. De quantos modos diferentes ele pode se vestir? Para saber essas combinações é necessário utilizar as propriedades da análise combinatória.

Binômio de Newton

Binômio de Newton

Denomina-se Binômio de Newton , a todo binômio da forma (a + b)ⁿ , sendo n um número natural .

Exemplo: B = (3x - 2y)⁴ ( onde a = 3x, b = -2y e n = 4 [grau do binômio] ).

Nota 1: Isaac Newton - físico e matemático inglês(1642 - 1727). Suas contribuições à Matemática, estão reunidas na monumental obra Principia Mathematica, escrita em 1687.

Exemplos de desenvolvimento de binômios de Newton : a) (a + b)² = a² + 2ab + b² b) (a + b)³ = a³ + 3 a²b + 3ab² + b³ c) (a + b)⁴ = a⁴ + 4 a³b + 6 a²b² + 4ab³ + b⁴ d) (a + b)⁵ = a⁵ + 5 a⁴b + 10 a³b² + 10 a²b³ + 5ab⁴ + b⁵

Nota 2: Não é necessário memorizar as fórmulas acima, já que elas possuem uma lei de formação bem definida, senão vejamos:

Raciocínio Lógico - Triangulo de Pascal

O triângulo de pascal é dividido em linhas e colunas, e é composto de números binomiais.

Em cada número binomial , n, o numerador, está relacionado ao número da linha e k, o denominador, ao número da coluna.

Observe que na quinta linha temos 5 números binomiais, todos eles com numerador igual a 4.

Veja também que na terceira coluna todos os números binomiais possuem 2 como denominador.

Resumindo, o numerador de todos os números binomiais de uma determinada linha é o mesmo, assim como o denominador de todos os números binomiais de uma certa coluna é igual ao número da coluna.

Linhas e colunas começam em 0.

As linhas de um Triângulo de Pascal possuem uma quantidade finita de elementos, que é igual ao número da linha mais 1. Por exemplo, a quinta linha, que é a de número 4, possui 5 elementos.

Já a quantidade de elementos por coluna é infinita, pois o número de linhas do Triângulo de Pascal também é infinito.

Simbologia Matemática

Neste post, vamos observar os principais símbolos matemáticos usados atualmente

Símbolos lógicos matemáticos (Usado no Raciocínio Lógico)

~ = negação
^ = e
v = ou
→ = se, então
↔ = se e somente se
/ = tal que
= existe

Raciocínio Lógico - Testes

Testes de Raciocínio Lógico

Teste seus conhecimentos! 1. Dizer que não é verdade que Celina é bonita ou Cristina não é loira, é logicamente equivalente a dizer que é verdade que: a) Celina não é bonita ou Cristina não é loira b) Celina não é bonita e Cristina é loira c) Celina é bonita ou Cristina é loira d) Celina é bonita e Cristina é loira e) Celina não é bonita e Cristina não é loira   2. Ou Y = X, ou X = Z, mas não ambos. Se X = W, então Y = W. Ora X = W. Logo: a) X ≠ Z b) X ≠ Y c) Z = Y d) Z = X e) W ≠ Y 3. Se Maria não anda sozinha, então Pedro sabe costurar. Se Maria anda sozinha, então ou Joana estuda ou Manoel trabalha. Se Manoel trabalha, Teresa faz ginástica. Mas Teresa faz ginástica se e somente se não for verdade que Ferdinando não tem uma camera. Ora, Ferdinando não tem uma camera e Joana não estuda. Logo: a) Maria não anda sozinha e Manoel trabalha b) Joana não estuda e Manoel trabalha c) Ferdinando não tem uma camera e Teresa faz ginástica d) Pedro não sabe costurar ou Maria anda sozinha e) Pedro sabe costurar e Manoel não trabalha.

Resumão Raciocínio Lógico

Como Estudar Raciocínio Lógico para Concursos

As questões de Raciocínio Lógico sempre vão ser compostas por proposições que provam, dão suporte, dão razão a algo, ou seja, são afirmações que expressam um pensamento de sentindo completo. Essas proposições podem ter um sentindo positivo ou negativo. Exemplo 1: João anda de bicicleta. Exemplo 2: Maria não gosta de banana. Tanto o exemplo 1 quanto o 2 caracterizam uma afirmação/proposição. A base das estruturas lógicas é saber o que é verdade ou mentira (verdadeiro/falso). Os resultados das proposições SEMPRE tem que dar verdadeiro. Há alguns princípios básicos: Contradição: Nenhuma proposição pode ser verdadeira e falsa ao mesmo tempo. Terceiro Excluído: Dadas duas proposições lógicas contraditórias somente uma delas é verdadeira. Uma proposição ou é verdadeira ou é falsa, não há um terceiro valor lógico (“mais ou menos”, meio verdade ou meio mentira). Ex. Estudar é fácil. (o contrário seria: “Estudar é difícil”. Não existe meio termo, ou estudar é fácil ou estudar é difícil).

Propriedades de Geometria Plana

Área

Área é um conceito matemático que pode ser definida como quantidade de espaço bidimensional, ou seja, sua superfície. 

Existem várias unidades de medida de área, sendo a mais utilizada na matemática o metro quadrado (m²). São também muito usadas as medidas agrárias: o Are, que equivale a cem metros quadrados; e seu múltiplo hectare, que equivale a dez mil metros quadrados. Outras unidades de medida de área são o acre, que equivale a 4 046,85642 m² e o alqueire, que equivale a 24 200 m².
Na geografia e na cartografia, o termo "área" corresponde à projeção em um plano horizontal de uma parte da superfície. Assim, a superfície de uma montanha poderá ser inclinada, mas a sua área é sempre medida num plano horizontal.

A História da Geometria Plana

A Historia da Geometria Plana

A Geometria tem origem provável na agronomia ou medição de terrenos, segundo o historiador grego Heródoto (Sec. V a.C. ). Contudo, é certo que civilizações antigas possuíam conhecimentos de natureza geométrica, da Babilônia à China, passando pelas civilizações Hindus.

O termo "geometria" deriva do grego geometrein, que significa medição da terra (geo=terra, metrein=medição).

Em tempos antigos, a geometria era uma ciência empírica, uma coleção de regras práticas para obter resultados aproximados. Apesar disso, estes conhecimentos foram utilizados nas construções das pirâmides e templos Babilônicos e Egípcios.

Mas é sem dúvida com gregos, começando com Tales de Mileto (624-547 a.C.), que a geometria é estabelecida como teoria dedutiva. O trabalho de sistematização em geometria iniciado por Tales é continuado nos séculos posteriores, nomeadamente pelos pitagóricos.

Não existem documentos matemáticos de produção pitagórica, nem é possível saber-se exatamente a quem atribuir as descobertas matemáticas dos pitagóricos na aritmética e na geometria.

Mais Tarde, Platão se interessa muito pela matemática, em especial pela geometria, evidenciando, ao longo do ensino, a necessidade de demonstrações rigorosas dedutivas, e não pela verificação experimental.

Esta concepção é exemplarmente desenvolvida pelo discípulo da escola platônica Euclides de Alexandria (325-285 a.C.), no tratado Elementos publicado por volta de 300 a.C., em treze volumes ou livros.

A geometria denominada de Euclidiana surge assim em homenagem a Euclides; Nos seus treze livros Euclides baseia-se nos seus precedentes gregos: os pitagóricos, Eudóxio, Taeteto. 

Mas Euclides mais do que expor as teorias destes mestres organiza as matérias de um modo sistemático a partir de princípios e definições, procedendo ao seu desenvolvimento por via dedutiva.

Inaugurava assim o que , de maneira brilhante, domina o mundo matemático durante mais de vinte séculos, o chamado método axiomático, que inspiraram a humanidade, ao longo dos tempos e em muitos outros campos do saber, da moral, da política, e organizar as suas ideias segundo os mesmos princípios.

Lista de exercícios sistemas lineares

Ola a todos:

Tenho uma bela lista de exercícios sobre sistemas lineares, bom para nivel médio e superior, faça o download no link abaixo e divirta-se. 

Para pedidos, mande um e-mail para infofisexatas@gmail.com

Link abaixo

http://rapidshare.com/files/944644332/GABlistsegproblcontexsistlinear.doc

Os Polinômios

Para polinômios podemos encontrar várias definições diferentes como: Polinômio é uma expressão algébrica com todos os termos semelhantes reduzidos. Polinômio é um ou mais monômios separados por operações.
As duas podem ser aceitas, pois se pegarmos um polinômio encontraremos nele uma expressão algébrica e monômios separados por operações.

• 3xy é monômio, mas também considerado polinômio, assim podemos dividir os polinômios em monômios (apenas um monômio), binômio (dois monômios) e trinômio (três monômios).
• 3x + 5 é um polinômio e uma expressão algébrica.

Como os monômios, os polinômios também possuem grau e é assim que eles são separados. Para identificar o seu grau, basta observar o grau do maior monômio, esse será o grau do polinômio.

Com os polinômios podemos efetuar todas as operações: adição, subtração, divisão, multiplicação, potenciação.

Nas situações envolvendo cálculos algébricos, é de extrema importância a aplicação de regras nas operações entre os monômios. As situações a serem apresentadas abordarão a adição, a subtração e a multiplicação de polinômios.

Adição e Subtração

Considere os polinômios –2x² + 5x – 2 e –3x³ + 2x – 1. Vamos efetuar a adição e a subtração entre eles.

Adição

(–2x² + 5x – 2) + (–3x³ + 2x – 1) → eliminar os parênteses realizando o jogo de sinal

–2x² + 5x – 2 – 3x³ + 2x – 1 → reduzir os termos semelhantes

–2x² + 7x – 3x³ – 3 → ordenar de forma decrescente de acordo com a potência

–3x³ – 2x² + 7x – 3


Subtração

(–2x² + 5x – 2) – (–3x³ + 2x – 1) → eliminar os parênteses realizando o jogo de sinal

–2x² + 5x – 2 + 3x³ – 2x + 1 → reduzir os termos semelhantes

–2x² + 3x – 1 + 3x³ → ordenar de forma decrescente de acordo com a potência

3x³ – 2x² + 3x – 1



Multiplicação de polinômio por monômio

Para entendermos melhor, observe o exemplo:

(3x2) . (5x3 + 8x2 – x) → aplicar a propriedade distributiva da multiplicação

15x5 + 24x4 – 3x3


Multiplicação de polinômio por polinômio

Para efetuarmos a multiplicação de polinômio por polinômio também devemos utilizar a propriedade distributiva. Veja o exemplo:

(x – 1).(x2 + 2x - 6)


x2 .(x – 1) + 2x .(x – 1) – 6 . (x – 1)

(x³ – x²) + (2x² – 2x) – (6x – 6)

x³ – x² + 2x² – 2x – 6x + 6 → reduzindo os termos semelhantes.

x³ + x² – 8x + 6

Portanto, nas multiplicações entre monômios e polinômios aplicamos a propriedade distributiva da multiplicação.

Divisão inteira de polinómios

Calcule o quociente e o resto da divisão inteira de

A(x) = 4x3 + 8x2 + 1 por B(x) = 2x2 + 3x - 1.

Resolução: Recorde que o algoritmo da divisão inteira de polinómios permite calcular o quociente e o resto da divisão inteira de dois quaisquer polinómios. Neste caso obtemos:

e portanto
Q = 2x + 1 e R = 2 - x.

A Radiciação

Matematicamente, a raiz  de um número real não negativo x é o número real não negativo que, é uma operação inversa da potenciação. A raiz quadrada porque 4 × 4 = 16, e √2 = 1.41421... . As raízes quadradas são importantes para a resolução de equações quadráticas (equações do 2º grau), e tambem são usadas para calculo de geometria, como exemplo o triângulo de pitágoras. A extensão da função raiz quadrada a números negativos leva à criação dos números imaginários e ao corpo dos números complexos, porem, pela matematica Euclidiana, não se é usado a raiz com numeros negativos.
-->

O primeiro uso do símbolo da raiz quadrada remonta ao século XVI. Pensa-se que a sua origem está na letra rradix (em latim, raiz). minúscula, primeira letra de

As seguintes propriedades da função raiz quadrada são válidas para todos os números reais positivos x e y:

sempre que x ≥ y

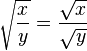
para todo o número real x (ver valor absoluto)

A aplicação da função raiz quadrada a um número racional dá em geral origem a um número algébrico; √x é racional se e somente se x puder ser representado por uma razão entre dois quadrados perfeitos. Por exemplo, √2 é irracional.
Geometricamente, a função raiz quadrada transforma a área de um quadrado no comprimento do seu lado.

Expressões Algebricas

Expressões algébricas são expressões matemáticas que apresentam letras e podem conter números, são também denominadas expressões literais. As letras constituem a parte variável das expressões, pois elas podem assumir qualquer valor numérico. No passado as letras foram pouco utilizadas na representação de números desconhecidos, atualmente as letras associadas a números constituem a base da álgebra e contribui de forma eficiente na resolução de várias situações matemáticas. Veja alguns exemplos de expressões algébricas:

2x – 5
3a + 2y
x² + 7x
5 + x – (5x – 2)
10y – 10x
a² – 2ab + b² 



Monômios

Em matemática, um monômio é um termo que contém apenas o produto de constantes e variáveis.
Intuitivamente, expressões como 1, a, e são monômios, mas expressões como x + 1, , e não são.
Um polinômio é definido com a soma de monômios. Por exemplo, no polinômio 2 + 4x³ + 2x² - x que é composto de 4 monônios, o grau mais alto dentre os 4 monômios é 3, pois corresponde ao expoente mais alto dos componentes do polinômio que é o expoente do monômio (x³). Portanto, um simples número pode ser considerado um monômio. Quer dizer, para ser um monômio, o coeficiente tem que sempre estar ligado a uma parte literal, como 3xy, onde o 3 que é coeficiente, esta multiplicando com a parte literal xy. Muito facil esse negocio de monômios.

 Polinômios

Em matemática, funções polinomiais ou polinômios são uma classe importante de funções simples e infinitamente diferenciáveis. Devido à natureza da sua estrutura, os polinómios são muito simples de se avaliar e por consequência são usados extensivamente em análise numérica. Então, para uma função ser considerada um polinômio, podemos pensar na possibilidade de somar os monômios, mas cuidado, para somar-mos os monômios, temos que saber se a parte literal é a mesma, pois partes literais diferentes não podem se somar.

A reta numerica....

Reta numérica é uma reta que representa o conjunto dos números reais. Ela pode estar tanto na horizontal quanto na vertical. No centro da reta fica o zero, que é sua origem.
No caso de a reta ser horizontal, temos do lado direito da origem os números positivos, e do lado esquerdo da origem os números negativos.
No caso de a reta ser vertical, temos acima da origem os números positivos, e, abaixo da origem, os números negativos.
A distância de um número ao zero é chamado de módulo ou valor absoluto. Ex: |-5| = 5; |5| = 5
Se um número é equidistante a outro em relação ao zero, dizemos que estes números são opostos. Ex: 2 e -2 são opostos.
Para saber mais: números naturais, números racionais, números inteiros, números irracionais, Conjuntos numéricos.
Entre um número inteiro e outro na reta existem infinitos outros números.