A Radiciação

Matematicamente, a raiz  de um número real não negativo x é o número real não negativo que, é uma operação inversa da potenciação. A raiz quadrada porque 4 × 4 = 16, e √2 = 1.41421... . As raízes quadradas são importantes para a resolução de equações quadráticas (equações do 2º grau), e tambem são usadas para calculo de geometria, como exemplo o triângulo de pitágoras. A extensão da função raiz quadrada a números negativos leva à criação dos números imaginários e ao corpo dos números complexos, porem, pela matematica Euclidiana, não se é usado a raiz com numeros negativos.
-->

O primeiro uso do símbolo da raiz quadrada remonta ao século XVI. Pensa-se que a sua origem está na letra rradix (em latim, raiz). minúscula, primeira letra de

As seguintes propriedades da função raiz quadrada são válidas para todos os números reais positivos x e y:

sempre que x ≥ y

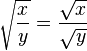
para todo o número real x (ver valor absoluto)

A aplicação da função raiz quadrada a um número racional dá em geral origem a um número algébrico; √x é racional se e somente se x puder ser representado por uma razão entre dois quadrados perfeitos. Por exemplo, √2 é irracional.
Geometricamente, a função raiz quadrada transforma a área de um quadrado no comprimento do seu lado.